基础自动驾驶规划算法知识总结梳理
search base
三种常见搜索算法的对比

BFS

dijkstra
dijkstra和BFS的区别,就是BFS只能适用于无权图,也就是认为每条路径都是一样的
如果对于一个无权图,使用BFS和Dijkstra是一样的效果
dijkstra等于是引入了一个两点之间移动的权重代价
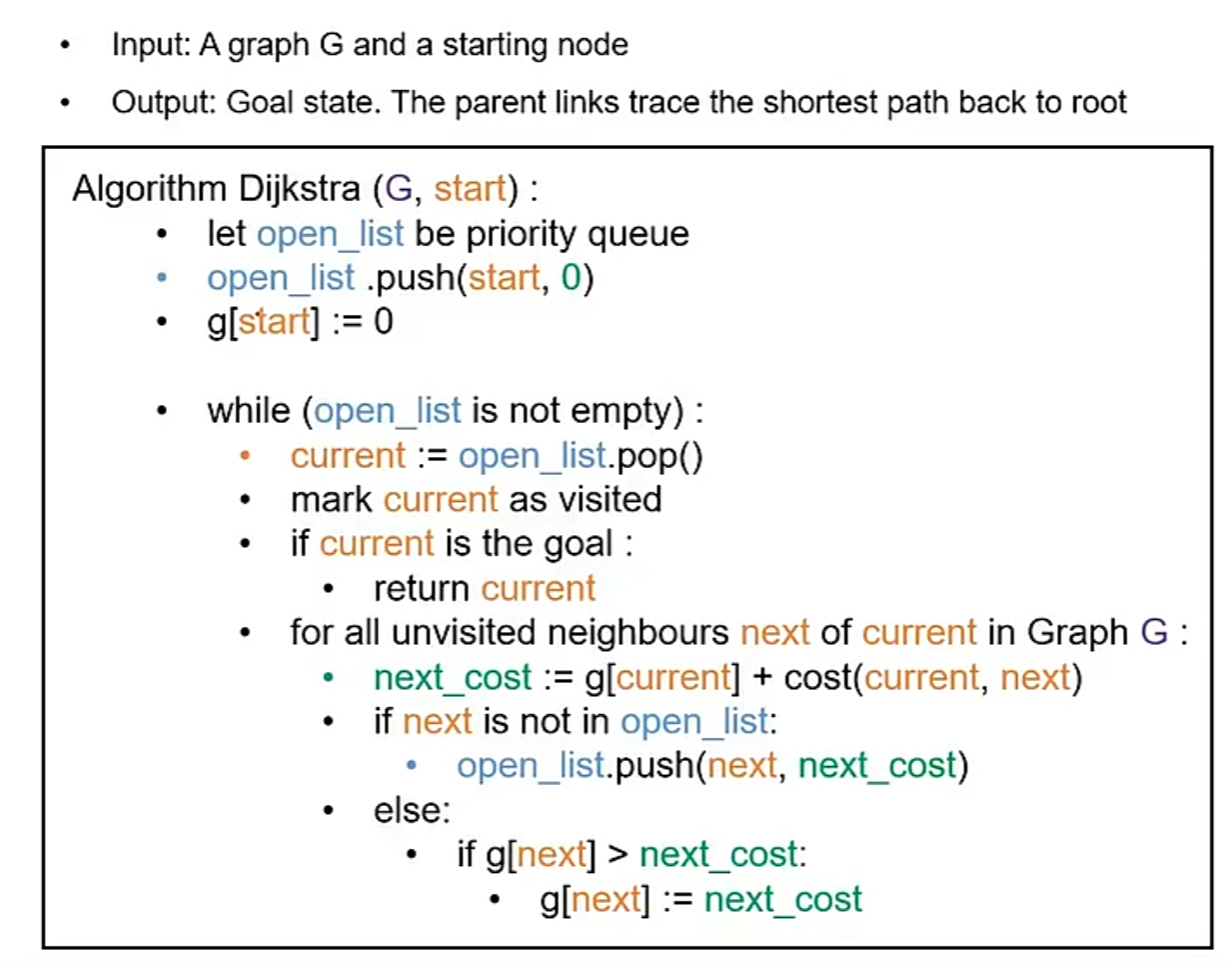
a*
相比较于dijkstra引入启发式函数,包含距离起始点的距离以及对目标点的距离估计,可以加快搜索时间,启发式函数可以引导搜索过程

astar常用的启发式函数:
欧几里得距离
就是简单的直线连接距离
曼哈顿距离
两个点之间xy坐标分别做差之和,就是走直线最短距离
启发式函数设计的原理:
保证启发式函数要小于等于两点之间的真实值,这样才能保证找到最优路径,
当启发式函数等于实际距离值,这样估计很准确,可以做到最优的搜索效率
对于四联通,欧几里得和曼哈顿都可以
对于八联通,曼哈顿不行,因为八联通可以走斜线,不能保证曼哈顿估计的距离小于实际距离

sample base
- 在图中生成种子(确定搜索起始点)
- 使用何种采样方式在图中采样
- 选择和哪个周围节点进行连接
- 选择那条边或者删除
PRM 随机概率路径图
优点:
- 具有概率完备性,如果点采的够多,一定可以取到最优路径
缺点:
- PRM是在完整的状态空间中进行采样的,相当于采样版本的dijkstra. 在当我们曲寻找特定初始点与目标点时,会有许多无用的扩展.
- 并且PRM是直接使用直线来连接采样点,不符合车辆的动力学约束
- 随机撒点,采样越多,对地图的信息掌握越多(这一步就删除所有碰撞点)
- 如果中间没有障碍物的话,连接相邻的(一定距离内)节点生成图(删除与障碍物碰撞的连接线)
- 在图中进行搜索,例如a*,dijkstra
下面sPRM是不剔除边,所有的都连接上

几种改进之后的PRM算法:
- k-nearest PRM
- 并不是连接一定距离之内的点,而是连接距离最近的前k个点
- Bounded-degree PRM 有界维度的PRM
- 相当于原始PRM和k-nearest PRM
- 首先按原始PRM进行取,如果一个节点的一定范围的连接点太多,则使用前k个点连接
- Variable-radius PRM 可变半径的PRM
- 把确定周围连接节点距离的半径r,设计成一个与采样点个数n相关的函数
- 如果采样点越多则减小,采样半径r
PRM* 一种Variable-radius PRM 可变半径的PRM

RRT 快速生成随机树
优点:
- 如果只是需要构建一条起点到终点的路径,相比于PRM,更为高效
缺点:
- 不具有概率完备性,只会和距离最近的采样点连接
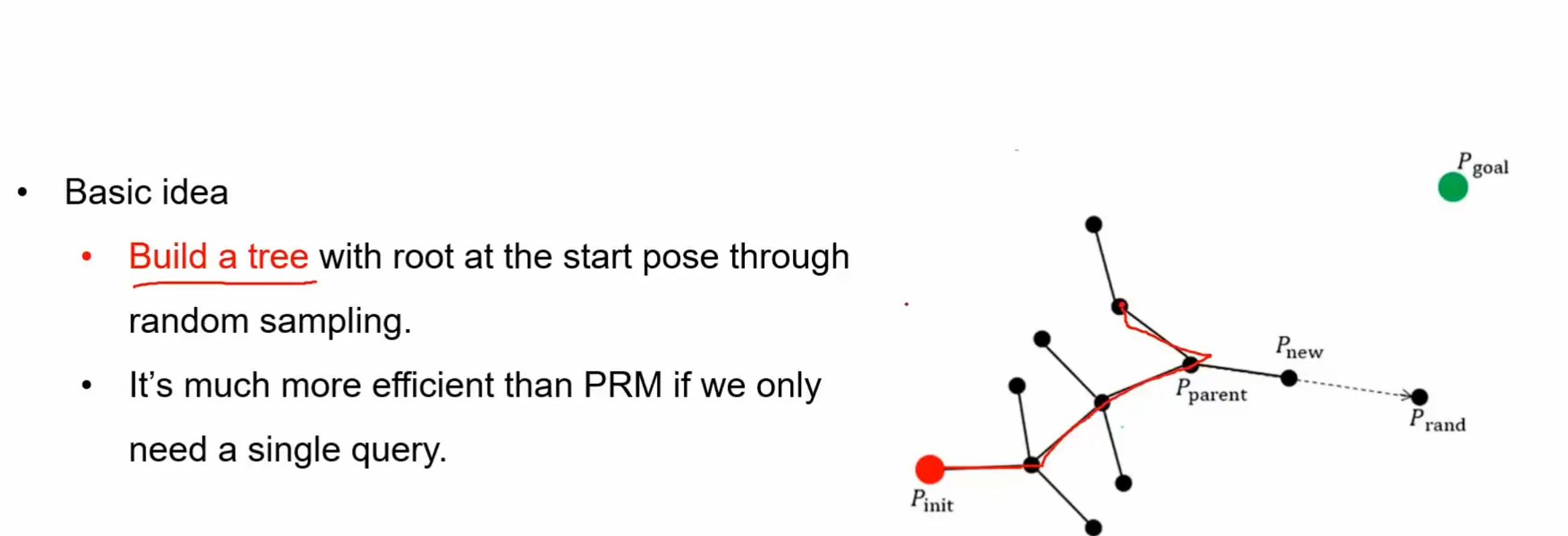
RRT所构建的是一个树,而不是图. 设置搜索起始点作为根节点
这样在只需要寻找两点之间的路径时,相比较于PRM搜索效率高很多
RRT 每次扩展节点时,都试图和目标节点做一次连接测试
- 首先初始化在RRT中要维护的两个结构,一个时包含顶点的集合V以及包含路径的集合E
- 开始主循环,设定最大采样次数n次
- 首先进行随机采样,得到X_rand
- 找到采样点中,距离当前书最近的节点,进行连接
- 并不是直接连接两点,而是向最近点方向走一个确定的步长
- 进行一个碰撞检测
- 判断连接终点是否能连接到树上

RRG 一种具备概率完备性的RRT变体
与RRT的主要不同对应于第九第十行:
- RRT中直接将最近节点向采样节点进行固定距离延申
- RRG改变了连接方式,每次不是直接向采样节点延申,而是考虑以采样点为中心的一个园,将圆内所有节点与采样点的无碰撞路径都进行连接,最终其实构建的是一个图

kinematic_based RRT 一种考虑车辆运动学的RRT
与RRT唯一的区别在于第五行,连接采样点时,基于某种运动学的方法连接(dubin RS曲线等)

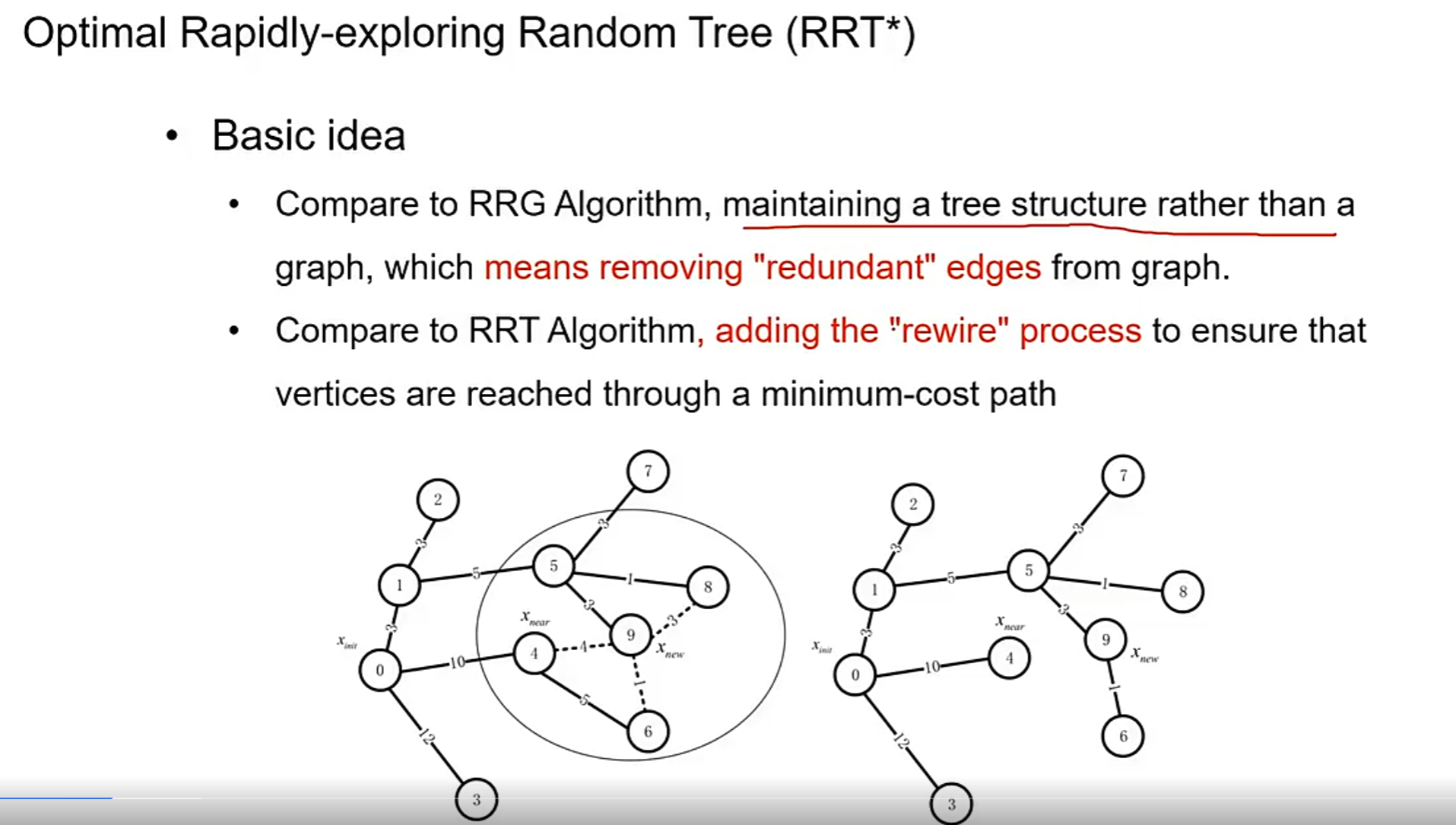
RRT* 优化快速随机生成树
与上面两种方法的对比
- 相比较与RRG,保留了树形的搜索结构,在结构中去掉了冗余的边
- 相比较与RRT,添加了一个重构的过程,确保顶点可以取到最小代价的路径
算法整体框架:

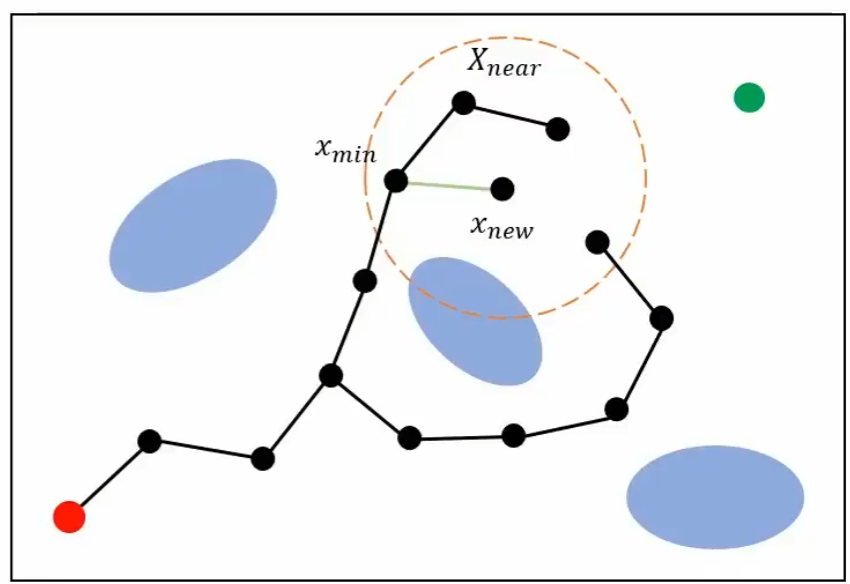
- 首先前面部分和普通的RPM一样,采样点,找距离树的最近点,确定最近点X_new
- 对于最近点利用RRG的特点,连接X_new,半径r内的所有节点
- 然后遍历半径r内的所有节点,选择cost(距离起点,距离x_new)最小的那个点来连接,这个点为x_min
- 进行修剪,遍历x_near(半径r内的点),查看是否可以通过x_new来得到一条剧起点cost更小的节点,如果有,就重新连接
CL-RRT closed-loop RRT
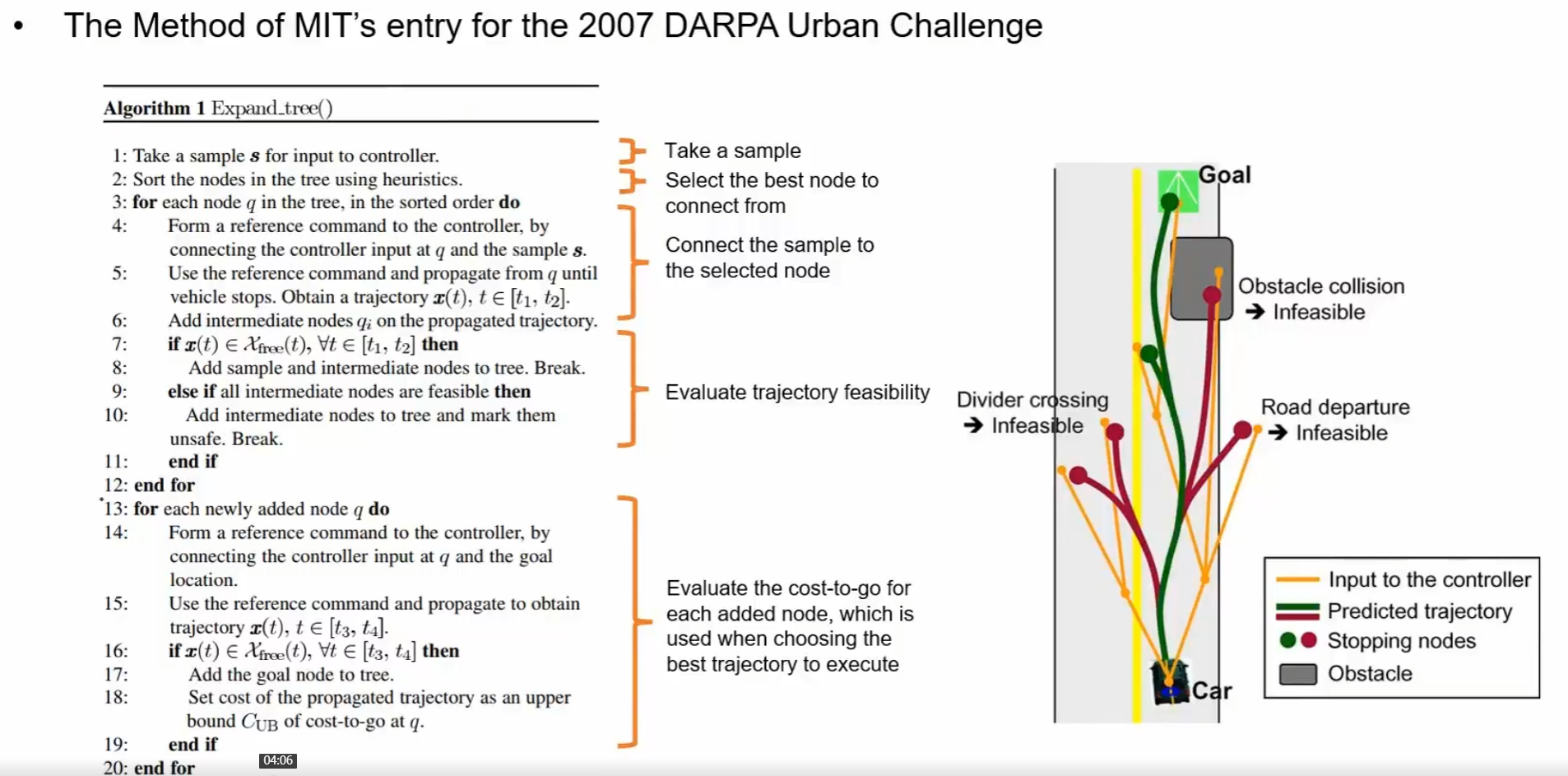
- 就是将RRT得到的一个折线结果,当成一个粗解,
- 然后使用控制器(解耦控制)
- 横向控制器(steer),纯跟踪控制器,输出为方向盘转角序列,也就是给出一条轨迹
- 根据粗解进行优化,从而进行控制
- 纵向控制器(speed),选择经典的pi控制器,输出速度序列
cl_rrt的采样策列
并不是在空间xy上进行采样,而是在r \theta 空间中进行采样,也就是在一个个同心圆以及不同角度上进行采样,相当于极坐标系采样
cl_rrt最近节点选择策略
使用dubins曲线来判断最近节点,而不是选择直线最短节点
kinematic base
dubins reeds-shepp曲线作为运动基元
dubins 只有6种组合可能

reeds-shepp 48种组合可能

多项式曲线作为运动基元
五次多项式 quintic polynomial solver
为什么使用五次多项式: 使用五次多项式对jerk进行优化,五次多项式得到的路径一定是最小的
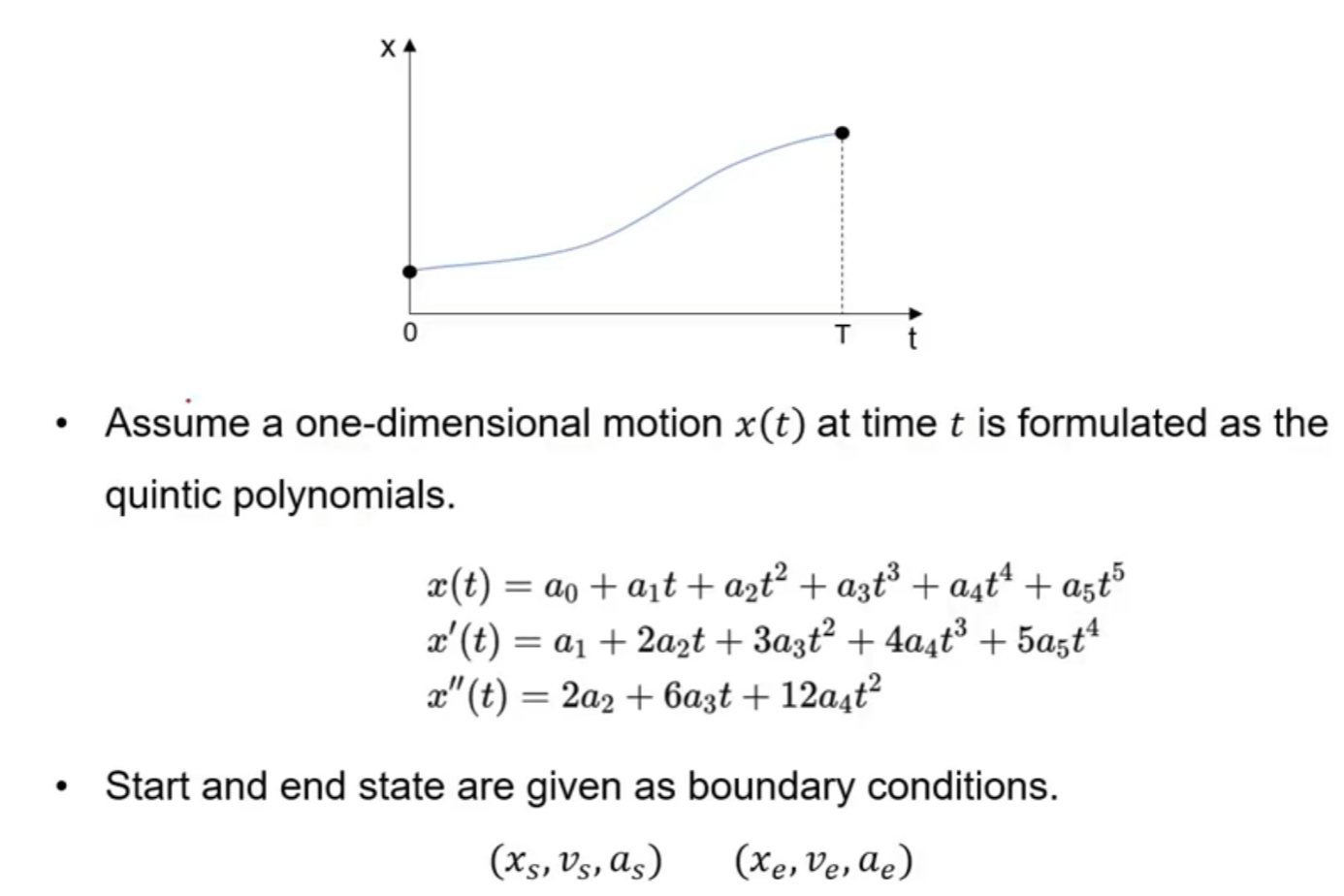
使用初始状态和终点状态,各三个一共六个参数,可以列出六个方程,确定五次多项式函数中的六个参数
- 所以说巡航轨迹规划中,不用考虑末状态的x值,只有五个参数,所以可以使用四次多项式来拟合
在st lt上进行采样
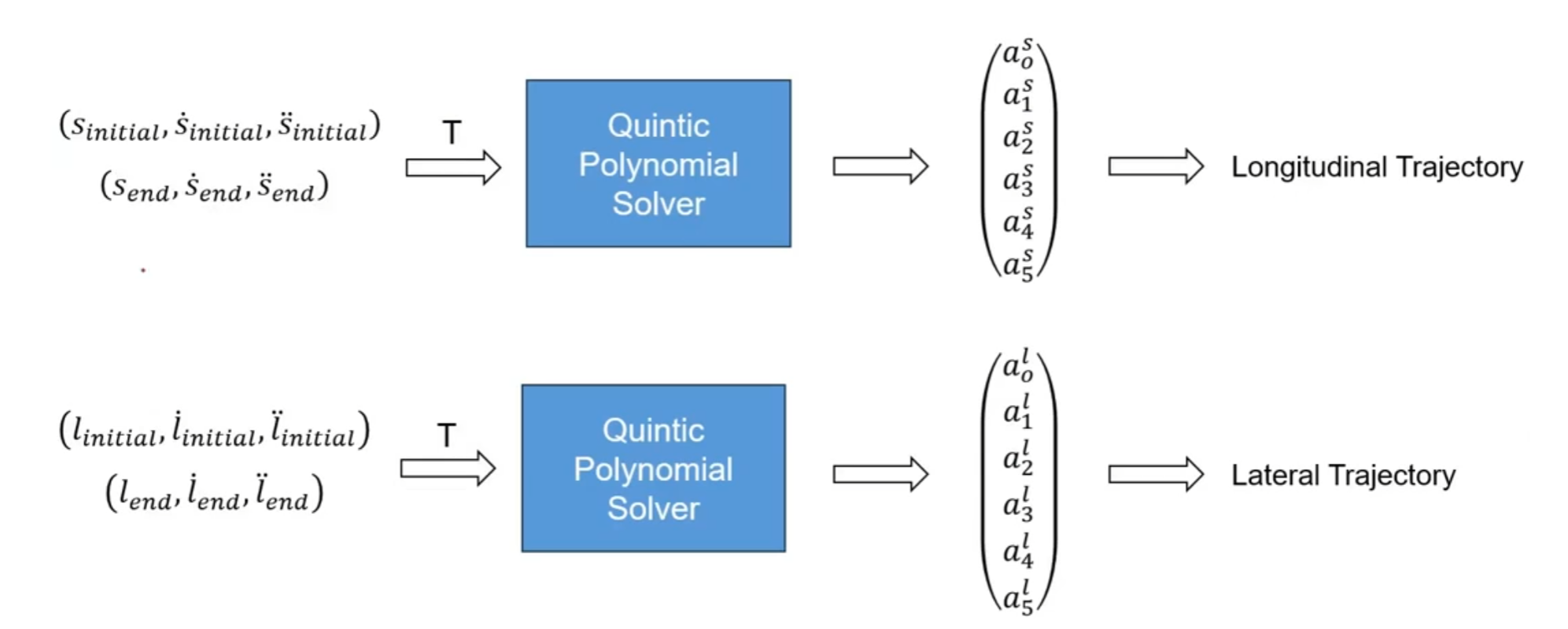
在sl st上进行采样
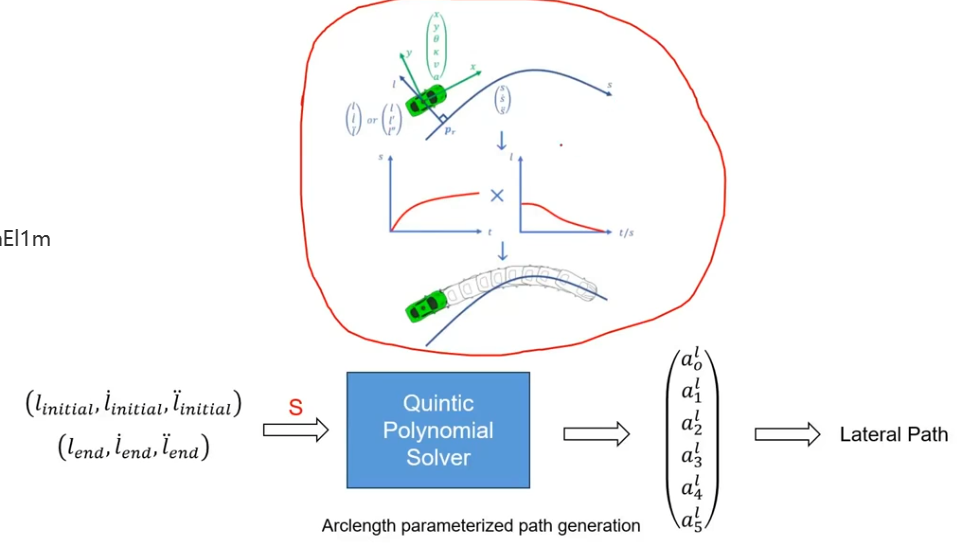
螺旋曲线作为运动基元(spiral Curve)
确定两个点之间的螺旋曲线,其实是一个BVP问题
曲率的定义,曲率的定义就是航向角关于弧长的变化率,所以曲率关于弧长的积分其实就是航向角的变化
- 螺旋曲线的定义:一个曲率对弧长的函数,在每一点的弧长处,我的曲率是多少
- **优点:**通过此特性,很容易限制路径曲率的变化
- 使用三次螺旋曲线来计算
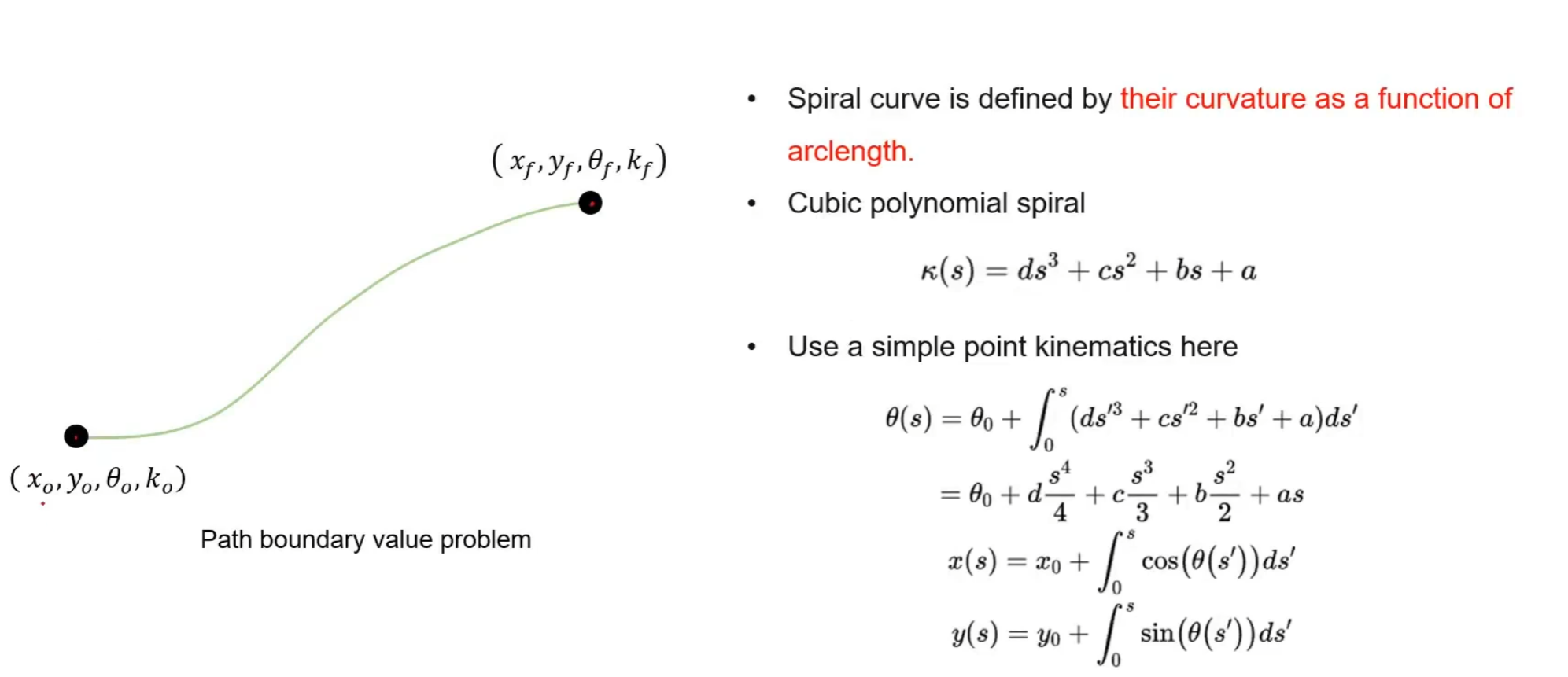
使用simpson方法求积分
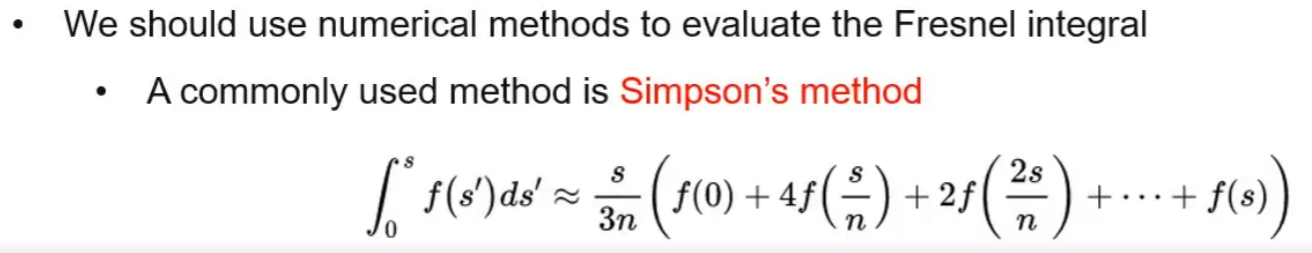
使用一个二次函数来近似原函数的值:
使用近似三个点来拟合出一条二次曲线,然后使用红色曲线积分值来近似蓝色曲线的积分值
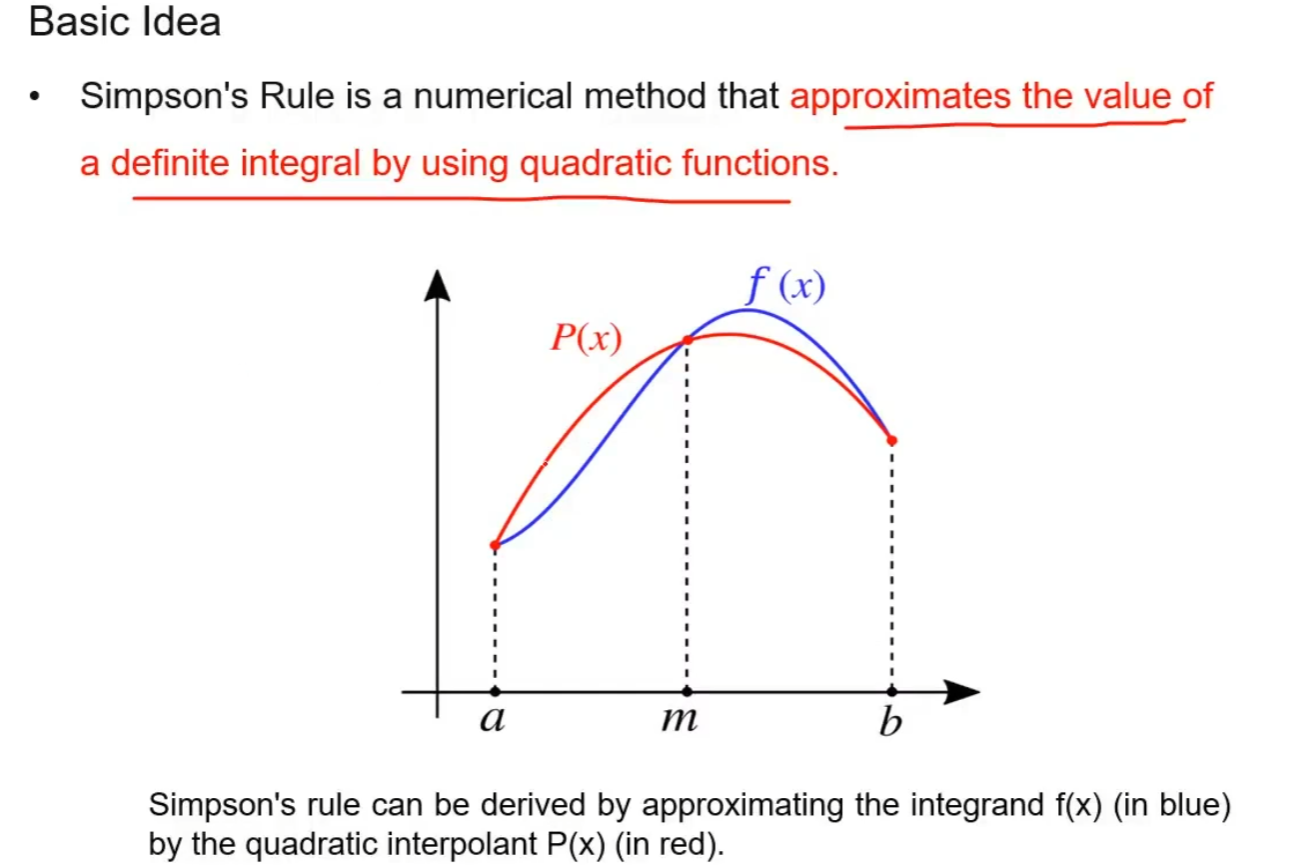
具体怎么计算求螺旋曲线参数,还是要看视频啊
混合a*
hA*中,在同一个栅格中保存一个最优解
混合a*一般是找不到最优解,因为有剪枝操作,并且是在控制空间进行采样的,例如只有方向盘转角的最大最小值,0,无法采样到最优的路径
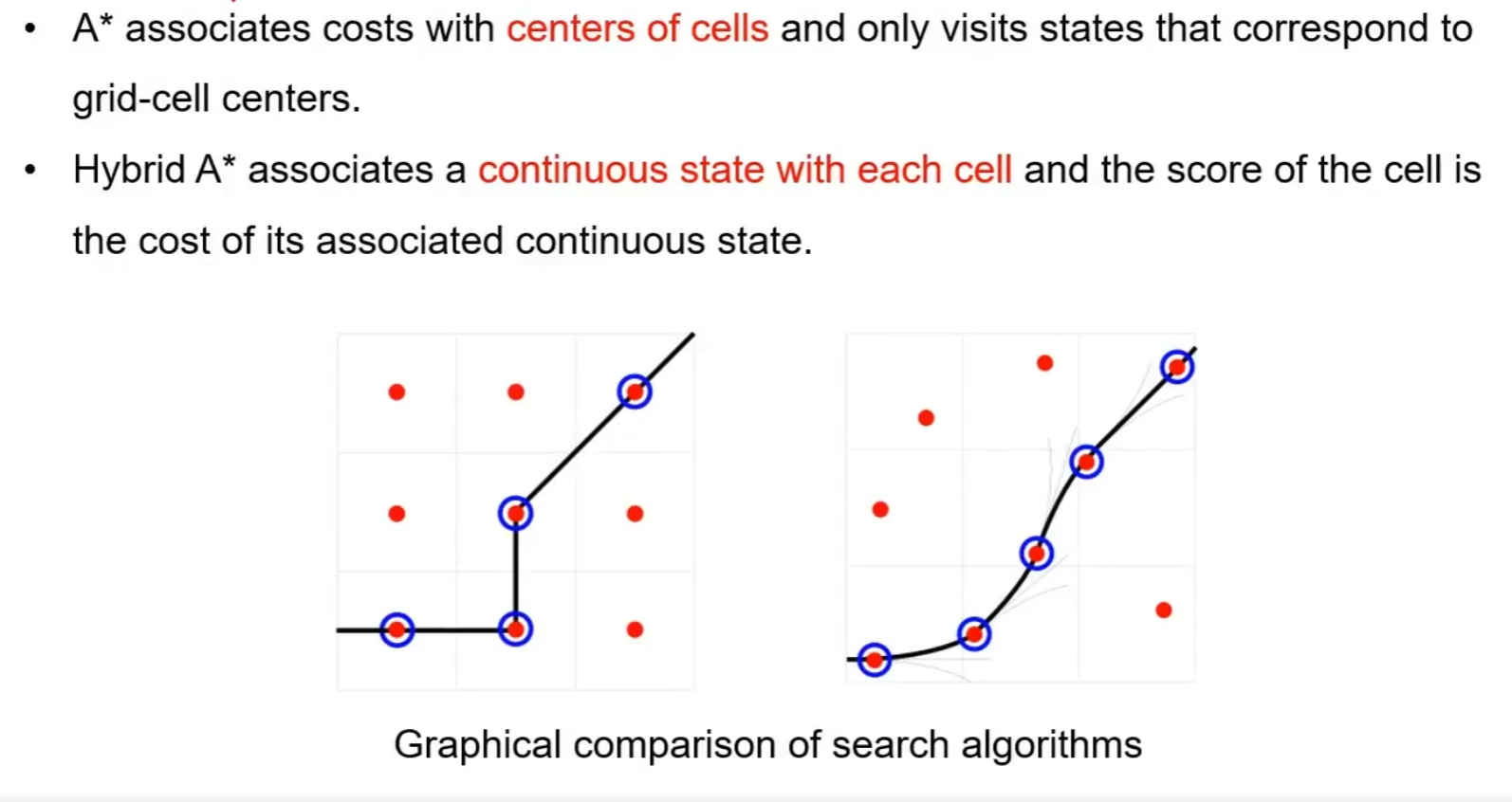

混合a*的两种启发式函数设计
不考虑障碍物的启发式函数
- 考虑车辆的运动学约束,不考虑障碍物
- 使用reeds-shepp曲线长度来作为启发式距离
- 可以满足启发式距离小于 < 实际距离
考虑障碍物的启发式函数
- 忽略车辆的运动学特征,只考虑环境中的障碍物
- 可以使用简单的a*作为启发式函数
同时使用上面两种启发式函数,通过调整权重,加速搜索
一种分层规划的思想
- 首先使用混合a*来生成一个粗略的解
- 使用优化的方法在局部进行调整
-
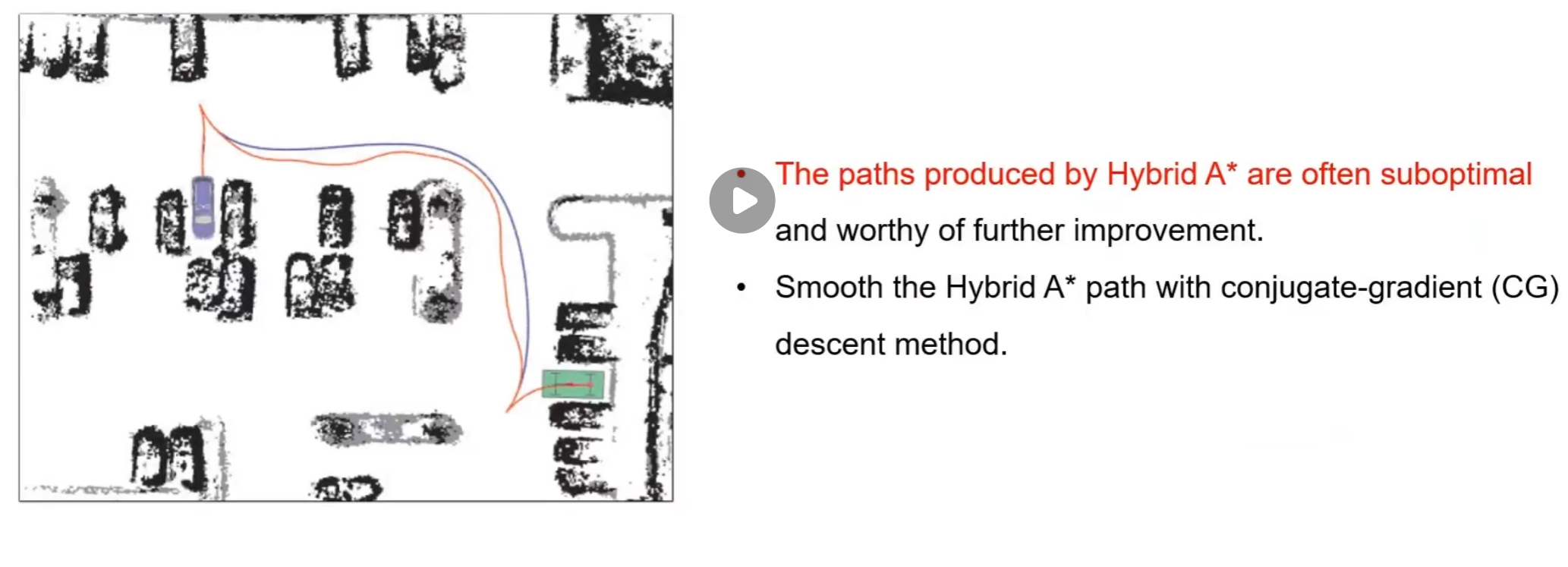
State Lattice
一种基于逆向运动学的规划方法
- 首先在fernet坐标系下进行采样
- 在frenet下采样,一般用五次多项式拟合
- 在cartesian坐标系采样(),一般使用三次螺旋曲线
- 解决BVP问题,使用五次多项式拟合,获得
- 计算每条路径的cost值
- 选择最优路径
lattice 常用的cost
- safety
- smoothness
- centerline attraction
final:
正向运动学和逆向运动学方法的对比
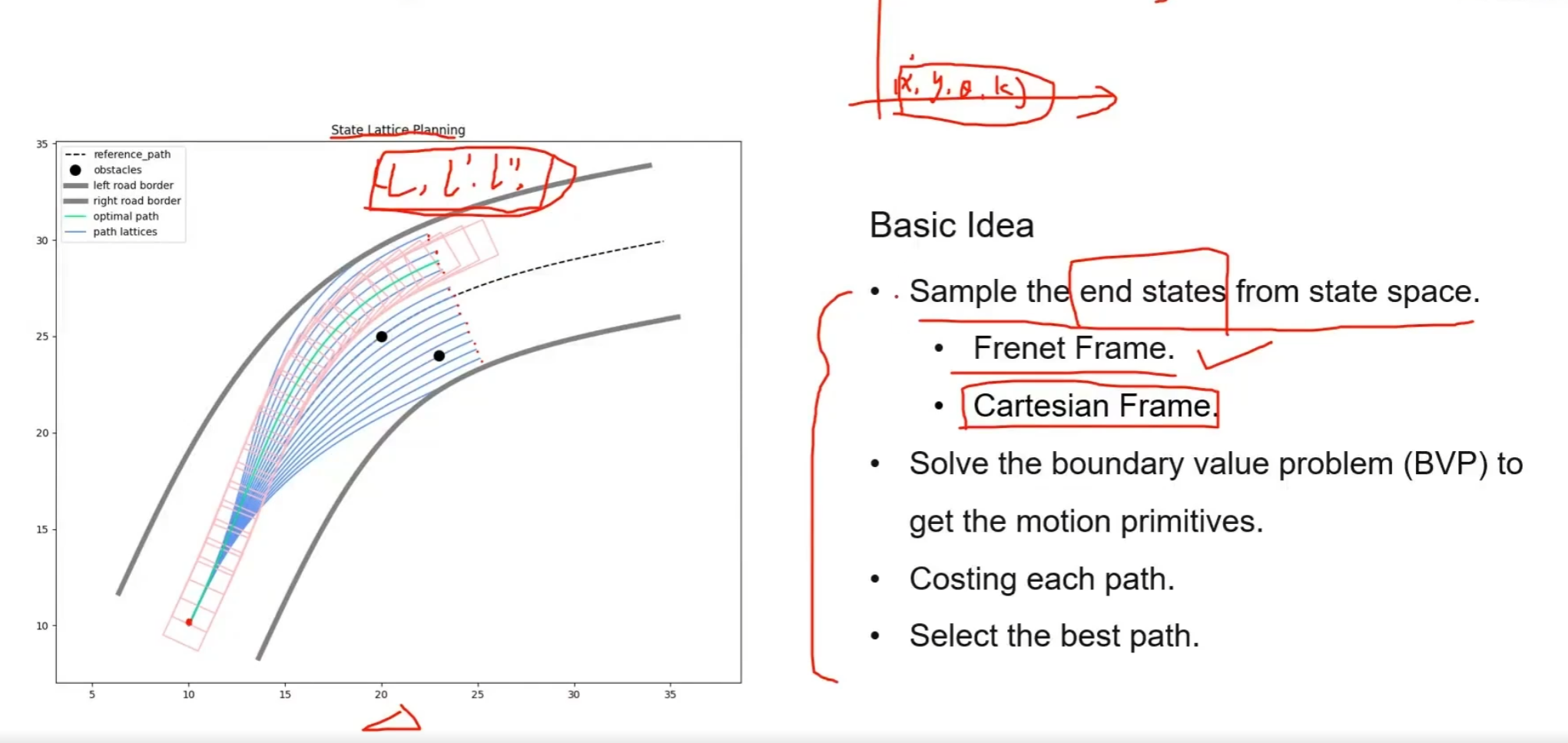
正向运动学采样:在控制空间进行采样,给定控制量,进行正向推断
逆向运动学采样:在状态空间进行采样,给定初始状态和末状态,推断中间状态
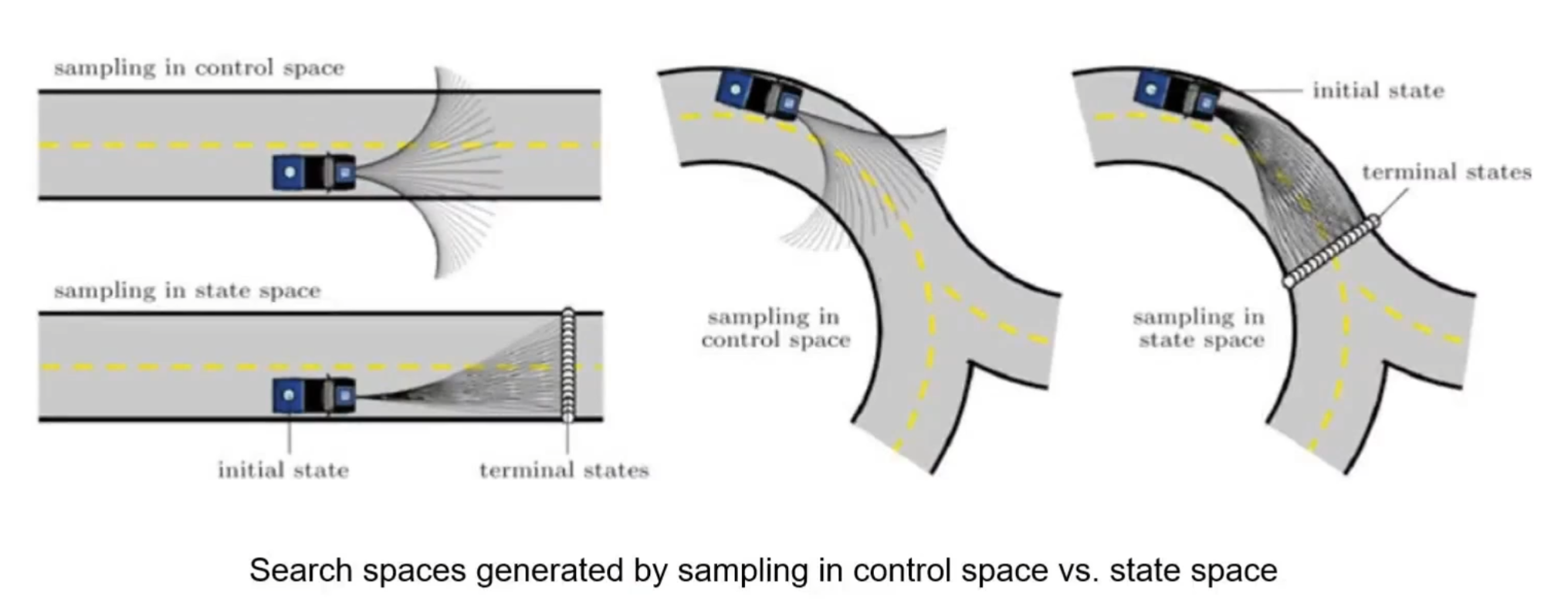
正向运动学采样-泊车
- 优点:易于计算,给定初始状态量和控制量,整个轨迹都可以根据运动学模型推断出来
- 缺点:缺少对于终点的指引,依赖启发式函数来确定搜索的方向
- 对环境的探索能力更强
逆向运动学采样-结构化道路
- 优点:强引导性,直接对目标位置进行采样
- 缺点:难以计算,需要计算一个BVP问题
- 采样的规则需要小心设定(例如遇到障碍物,采样的范围等)
optimizer base
数值优化基础
优化问题描述

-
目的:为了最小化一个函数,称为object/cost function
-
X为一个优化变量/向量,多个变量
-
s为x的取值范围,称为一个feasible region,一般会对约束进行拆分
- 等式约束
- 不等式约束
局部最优和全局最优:
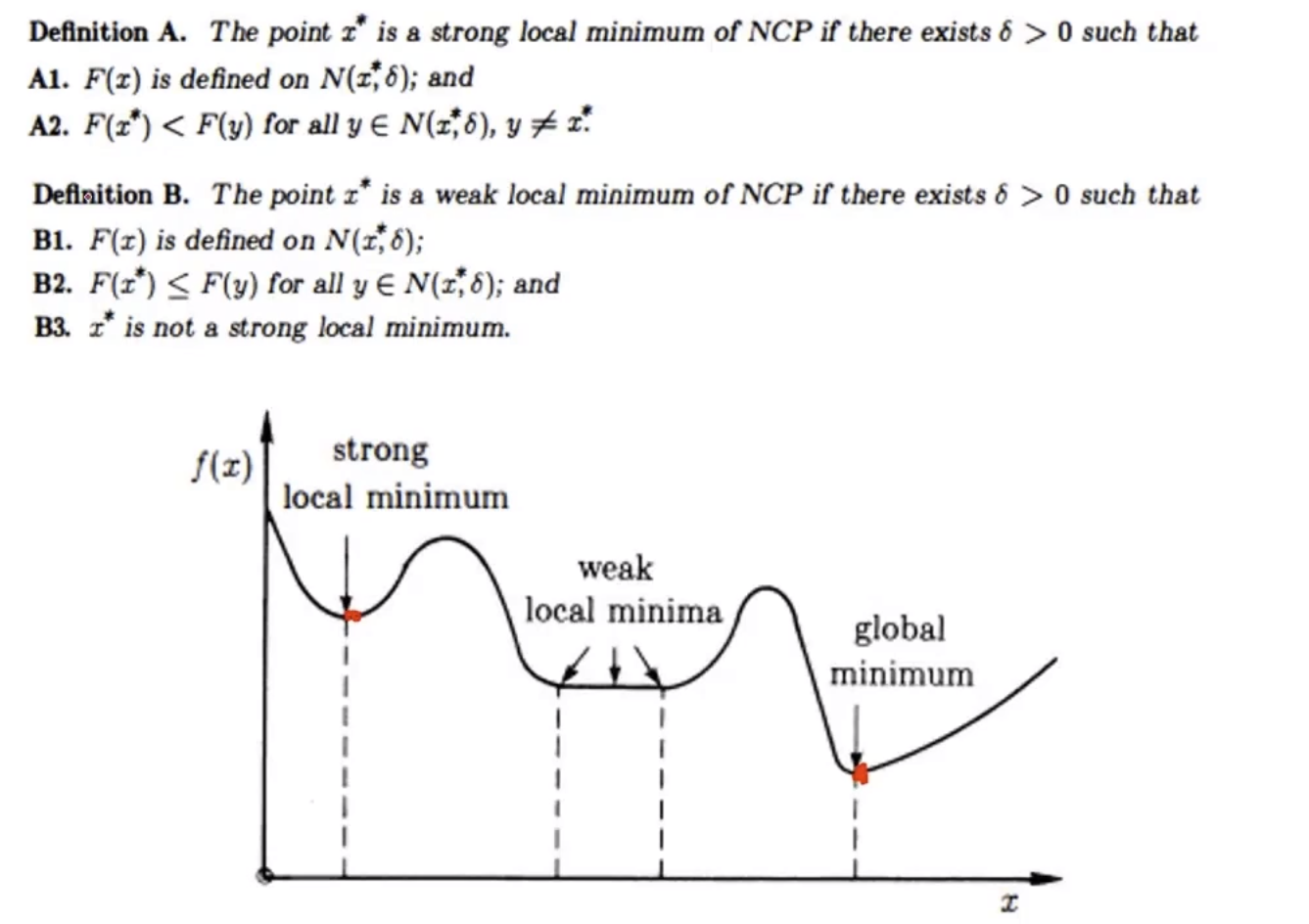
- 强局部最优,必须要小于周围值
- 弱局部最优,小于等于局部值
无约束优化(关键是如何选择迭代下降方向)
对于无约束问题,我们最小化函数只取决于优化变量,并且优化变量无限制
对于一个无约束问题:解是局部最优解的一个必要条件为,当前解的梯度为0
常见的无约束问题求解方法:
梯度下降-1阶雅可比矩阵:下降方向为梯度反方向, 下降步长由线性搜索确定
在远离极小值的位置下降跟快,在极小值附近下降很慢
高斯法-2阶黑塞矩阵: 下降方向由逼近的二次函数确定,下降步长由线性搜索确定/或者直接使用二次函数最小值。实际上是对目标函数F二次偏导的迭代
高司法在二阶导数的意义下,从函数凸性考虑,相当于不仅考虑坡度,还会考虑坡度的变化量
高斯牛顿法-1阶使用两个雅可比矩阵来近似黑塞矩阵:将原问题考虑为最小二乘法之后,也采用一阶导。
高斯牛顿为分解目标函数F为f*f后,对f的一次偏导的迭代。
其利用了目标函数的泰勒展开式把非线性函数的最小二乘化问题化为每次迭代的线性函数的最小二乘化问题。
缺点就是若初始点距离极小值点过远,迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值。
Levenberg-Marquart:
当μ大时相当于梯度下降法,μ小时相当于高斯牛顿法。
设置一个比较小的μ值,当发现目标函数反而增大时,将μ增大使用梯度下降法快速寻找,然后再将μ减小使用牛顿法进行寻找。
-
梯度下降法(1阶-是指只用到了梯度)
-
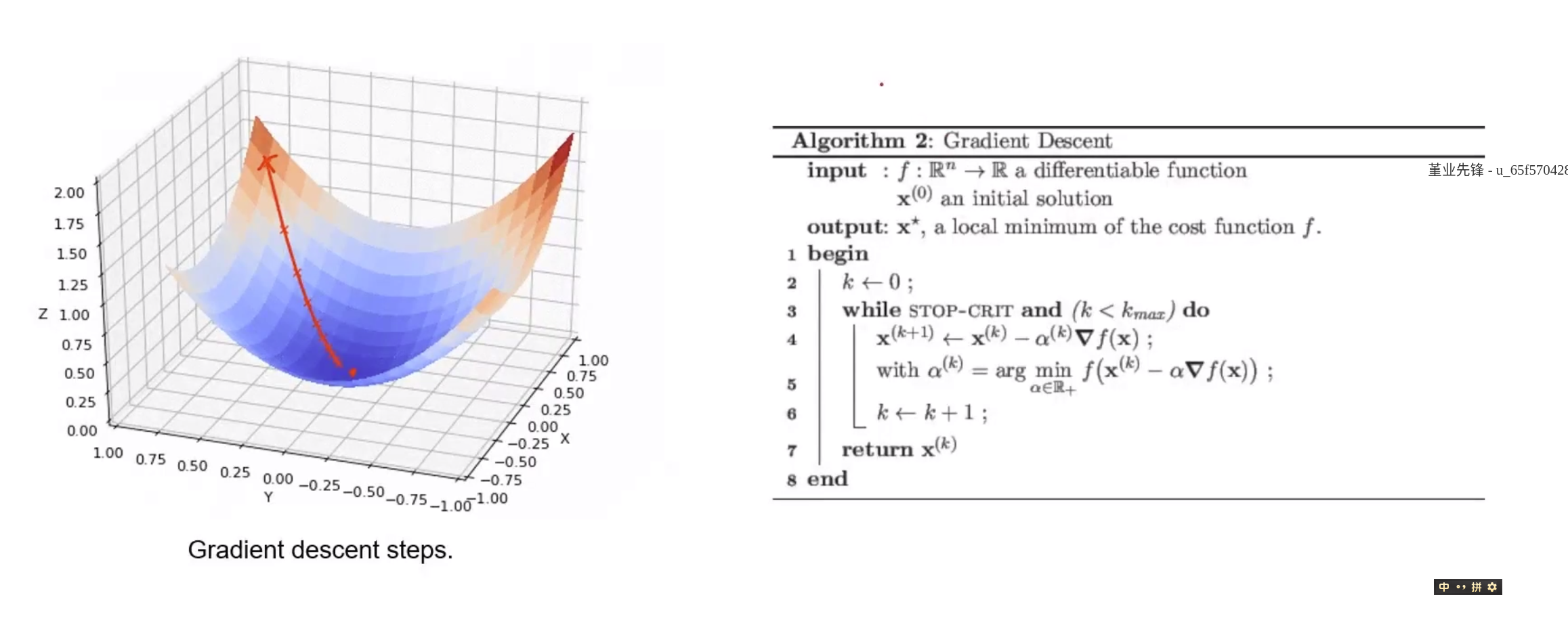
-

- 在每一迭代中,第k+1次迭代值为上一步向梯度反方向增加固定值,
- 梯度下降法的收敛条件,工程上,可能要求多个条件都满足时,停止优化
- 相邻两次下降优化变量x差值很小
- 相邻两次优化变量差值与上次优化变量的比值很小
- 相邻两次cost函数值差距很小,cost几乎不下降了
- 线性搜索确定每一次的下降步长
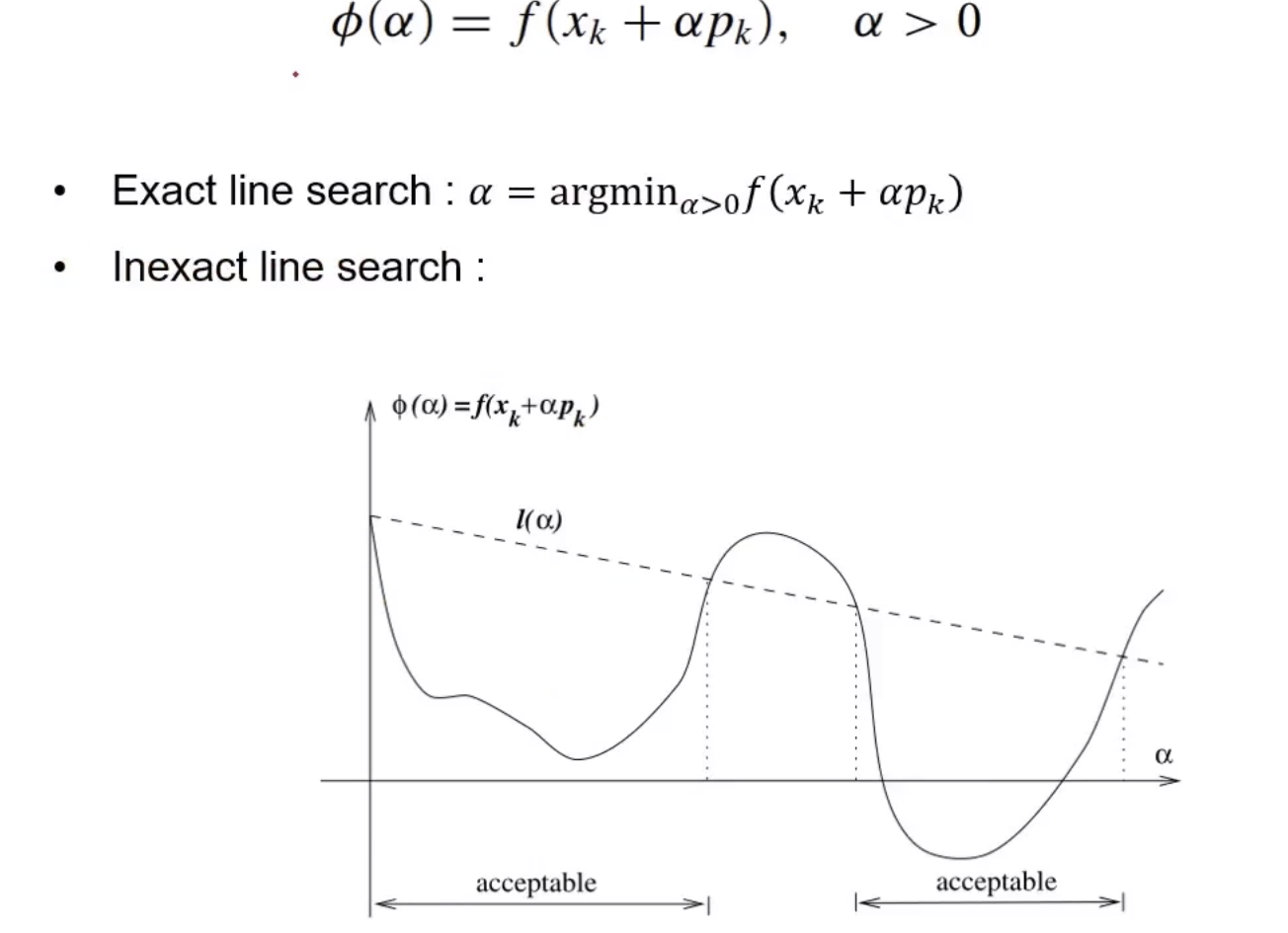 (P_k代表当前找到的搜索方向)
(P_k代表当前找到的搜索方向)- 精确线性搜索,不常用
- 在下降方向上(一个切面上),找到cost最小值,不一定是全局最优解,只是这个下降方向就不一定对
- 非精确的线性搜索,常用
- 不要求找到最小的cost点,见上面的图,只要在这个方向上,cost下降到一定水平,就可以
- 回溯的线性搜索
 (纵轴为cost值,这个图和上面的一样含义,只是换了个标志)
(纵轴为cost值,这个图和上面的一样含义,只是换了个标志)- 在当前位置找切线,只要当前确定的步长在上图的两个虚线之间,都是可以的
-
-
牛顿法(2阶)使用二次函数逼近原函数
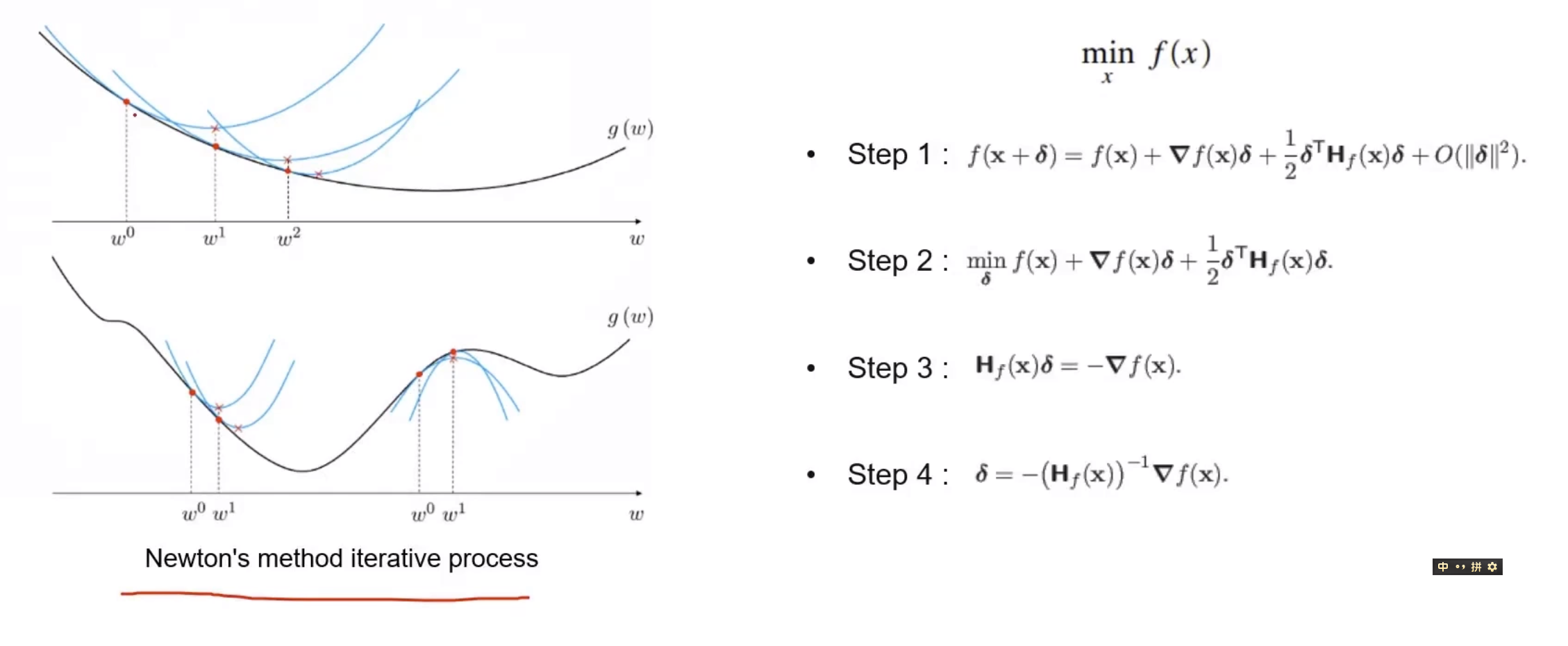

- 当前点做一个二阶泰勒展开,提取相邻曲线的信息
- 通过泰勒展开,利用逼近的二次函数下降方向,作为原函数的下降方向,
- 下降方向,下降方式为-黑塞矩阵逆乘以梯度
-
高斯牛顿法(2阶),面向最小二乘的类型,很多函数的平方和的最小值
-
-
levenberg-Marquardt(列文伯格-马夸尔特)-LM算法
- 当μ大时相当于梯度下降法,μ小时相当于高斯牛顿法。
- 设置一个比较小的μ值,当发现目标函数反而增大时,将μ增大使用梯度下降法快速寻找,然后再将μ减小使用牛顿法进行寻找。
二次规划
凸优化问题的描述:

对于一个优化函数,本事是凸函数,并且不等式函数约束也为凸函数,还有线性的等式约束,这就可以成为一个凸优化问题。
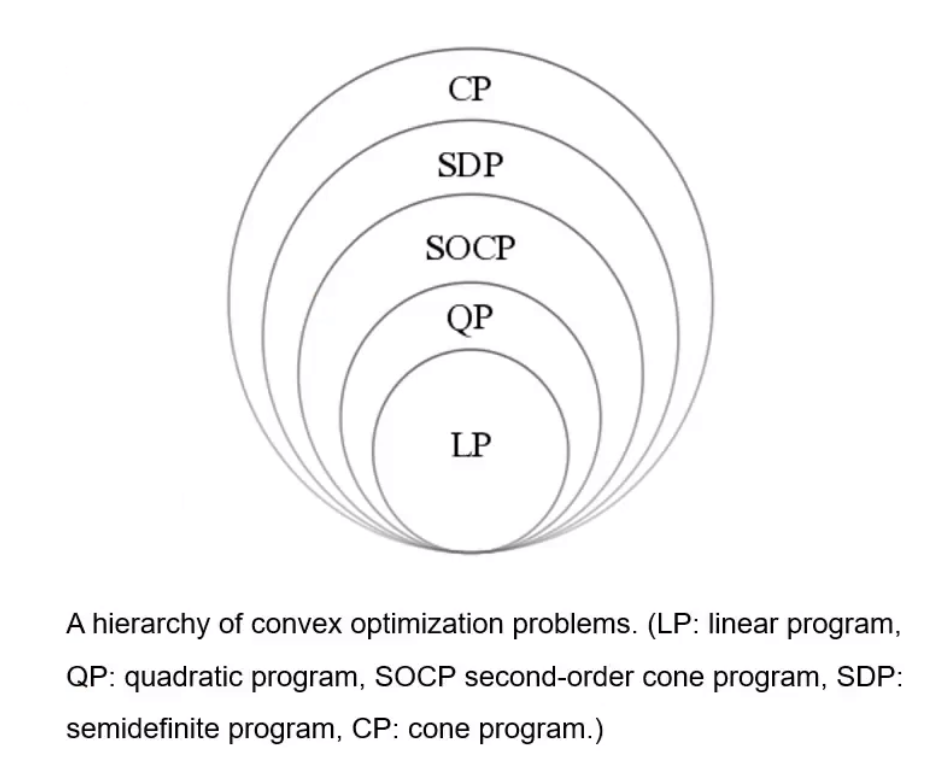
二次规划QP定义:

- cost function转为一个二次型表示]
- 所有的约束都要是线性的(包含等式和不等式约束)
osqp求解器中,没有单独的等式约束,等式表示为a≤x≤a
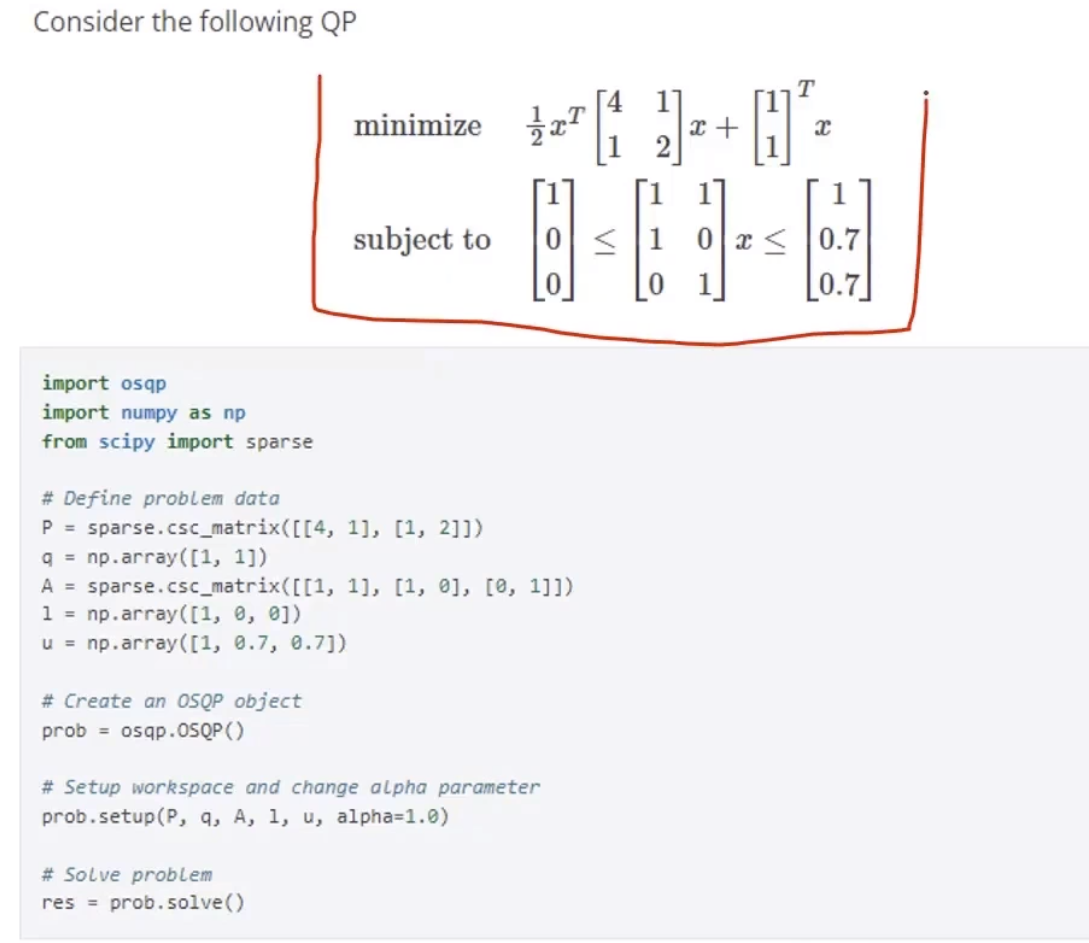
在osqp求解的矩阵输入中,稀疏矩阵P A需要表示为csc矩阵,压缩空间
非凸优化问题

常用的求解方式:
- SQP 拆解为多个QP问题
- IPM 内点可行域迭代
常用的非线性求解器Ipopt,使用内点法来求解
